Imagine this: you're organizing a birthday party and need to create party favors for the guests. You need to create goodie bags, and you need to split 318 pieces of candy among 3 people. You reach for your phone to use the calculator, but the phone's out of battery!
You need to divide a big number, but you don't have a calculator. Have no fear: use the long division method when you need to divide multi-digit numbers!
#1: Set up your problem
Decide what your divisor and dividend are. Your divisor is the number you're dividing by, and your dividend is the number being divided. If you need to split 318 pieces of candy among 3 people, 318 is the dividend, and your divisor is 3. The answer is called the quotient.
To use math's long division method, set up your problem by drawing a division bar (厂). Your divisor will go outside the bar on the left, and your dividend will go inside the box: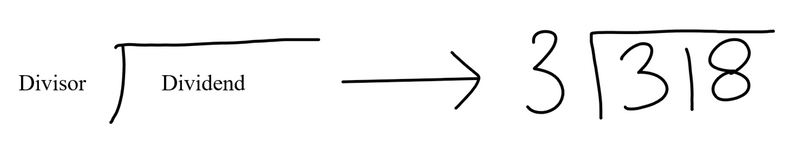 
#2: Focus on one digit at a time
Look at the divisor and the dividend. In the dividend, focus on the first digit. You'll be working with these numbers first. In this case, look at the 3 from the divisor and the 3 from the 318.
If your divisor has more than one digit, focus on the whole number. In your dividend, however, you'll continue to work with only one digit.
#3: "Multiply" to divide
What times 3 will equal 3?
3 will go into 3 one time — that means 3 x 1 = 3. This is perfect! Since the 3 outside the division sign goes into the 3 inside the division one time, write 1 on top of the 3 inside the division sign:
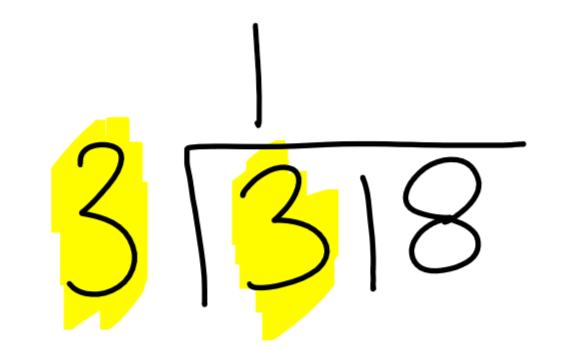
#4: Subtract and bring down
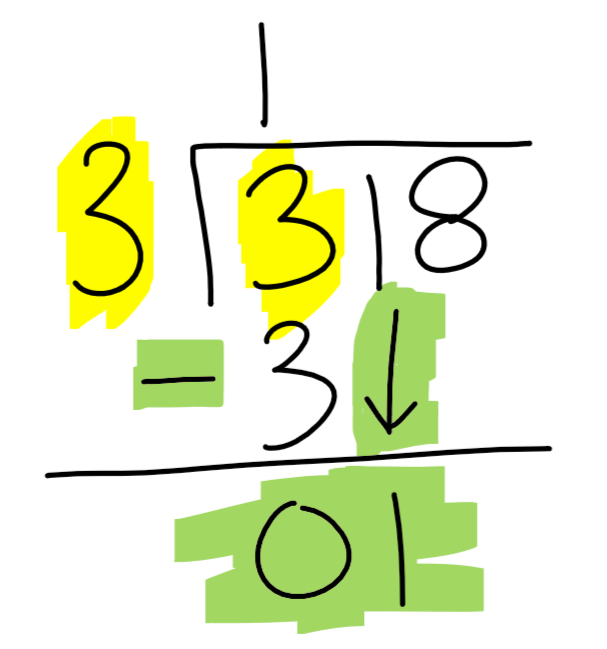
Subtract from the dividend. Since 3 x 3 = 1, subtract 3 (green) from the 3 in the dividend (yellow) to get 0. After subtracting, bring down the next digit, which is 1 in this case.
#5: Repeat the "multiply, subtract, and bring down" method
Use the "multiply, subtract, and bring down" method to solve for the next digit. In our example, think about how many times 3 goes into 1.
Continue the "multiply, subtract, and bring down" process until you've completed all the digits of the dividend.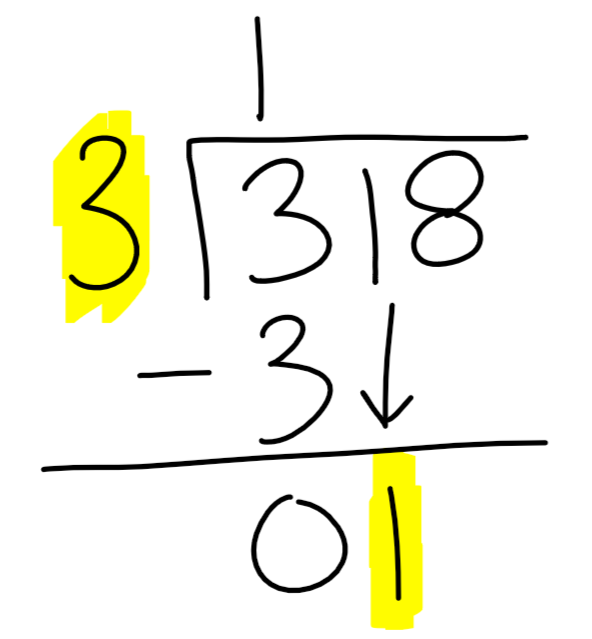 
Quiz
Solve the problem by continuing the "multiply subtract, and bring down" method! What is 318/3?
Special cases of the long division method
What if my divisor doesn't go into the dividend?
Write a '0' on top of that digit! For example, since 12 does not go into 2, write a '0' above 2:
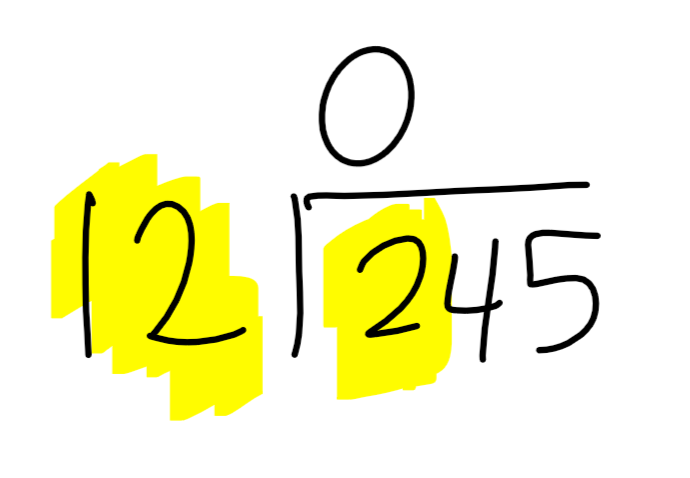
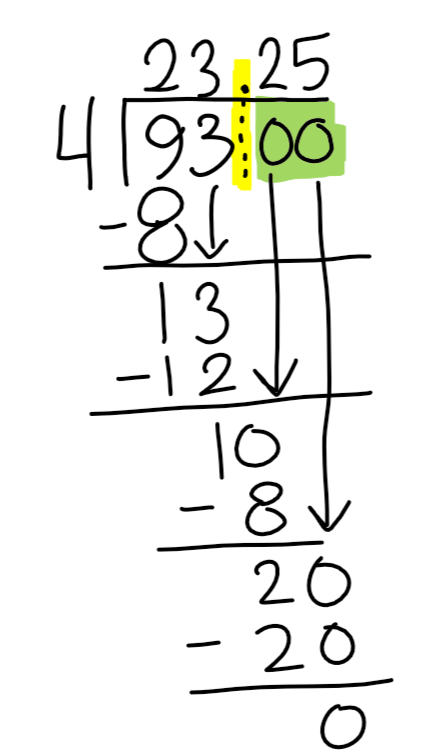
What if I reach the last digit of the dividend but still have a number other than 0?
Add a zero after the last digit of the dividend (green) and write a decimal point where the quotient/answer is (yellow). Then continue to solve until you get zero:
Quiz
A farmer has 428 pounds of soil and eight plots of land. She wants to distribute the soil evenly among the plots. Using math's long division method, what is 428/8?
Take Action
The long division method could be challenging at first, but with enough practice, the "multiply, subtract, and bring down" process will come naturally. These three simple steps repeat, so no matter what part you're on, you'll know what the next step will be.
Once you master the long division method, you're ready to take on more complex math problems!
Remember to practice long division!
Your feedback matters to us.
This Byte helped me better understand the topic.