How do I teach division to elementary math students?

Image by Wendy F. McMillian using clipart from PNGTree

Division is an essential concept for elementary math students to learn. It allows them to share things with others and divide tasks among group members.

When teaching students division, begin by having studentsthink about how they would share six chocolate chip cookies with a friend.

You could also have them think about how they may share a task when working as partners.

AI-generated image created by Wendy F. McMillian

Demonstrate division with a simple example problem:

Suppose you and your friend want to draw. Your friend doesn't have a pencil, while you have two pencils.

You decide to give one of your pencils to your friend. Now you both have one pencil each.

You have divided the pencils evenly between you and your friend. ✏️ / ✏️

Demonstrating the concept helps students understand how division results from "fair sharing", giving each person an equal part, or splitting something into equal parts.

There are many ways to teach division. Before students learn these ways, they need to know some words and definitions related to division:

• Dividend — the number that is being split into equal parts (in this case, 2 pencils)

• Divisor — the number you're using to split it with (2, because you're splitting the pencils across two people)

• Quotient — the result of the splitting or the answer to the division problem (2 people get one 1 pencil each)

• Remainder — what is left over when things can't be split into equal parts (if there are 3 pencils, 1 pencil will be left over)

Image created by Wendy F. McMillian

Students should understand fair sharing as dividing items into equal groups so that there is a one-to-one correspondence between groups.

For example, in the image above, 4 cupcakes are divided among four friends, so each person gets one cupcake. Therefore, 4 divided by 4 will equal 1.

Create fair shares by...well, sharing!

Use a scenario: For example, it's your birthday and you have a batch of cupcakes to share with your classmates. How can you make sure every classmate gets a cupcake?

Answer: By passing out cupcakes one at a time — one cupcake to one classmate!

Create fair shares by grouping.

Consider using a scenario that involves dividing objects into groups. For example, you have 12 strawberries that you want to share with four of your friends. How would you make sure each friend gets the same number of strawberries?

Have students work to solve this:

1. Split students into groups of four.

2. Give each group 12 buttons, disks, etc., that they can use as "strawberries".

3. Have one student give each student a "strawberry" until all are passed out.

The video below demonstrates how students could solve this. It shows 12 strawberries being shared between 4 friends, one at a time.

Video created by Wendy F. McMillian

Explain to students how they can ensure each friend gets an equal share when they give each friend a strawberry until all 12 strawberries are given out. Help them notice that each friend will get 3 strawberries each, meaning 12 divided by 4 equals 3.

Image created by Wendy F. McMillian

Students should also be shown that sometimes, things can't be divided evenly, leaving a remainder. Define a remainder as the amount left over after dividing, whichhappens when the first number doesn't divide evenly by the other.

For example, have students consider a picture like the one of the gingerbread cookies above. There are seven cookies in total. They'd have one left over if they wanted to divide the cookies with a friend. This is the remainder.

Have students try this out themselves in a group setting:

1. Split students into even groups (2, 4, 6, etc).

2. Give students an uneven number of items to divide (or share) (3, 5, 9, etc).

3. Have students divide the items until each student has the same number.

Get students to notice that there is one cookie remaining.

AI-generated image by Wendy F. McMillian

Help students see that multiplication and division are opposites.

Show them they can work backward when solving a division problem and consider the factors of numbers instead.

For example:

• What if you divide 30 by 6? What can you multiply 6 by to get to 30?

• 5 and 6 are factors of 30 — that is, numbers that multiply together to get another number.

Division is about finding the unknown factor. So, think about the numbers that will multiply to give you the number you're dividing.

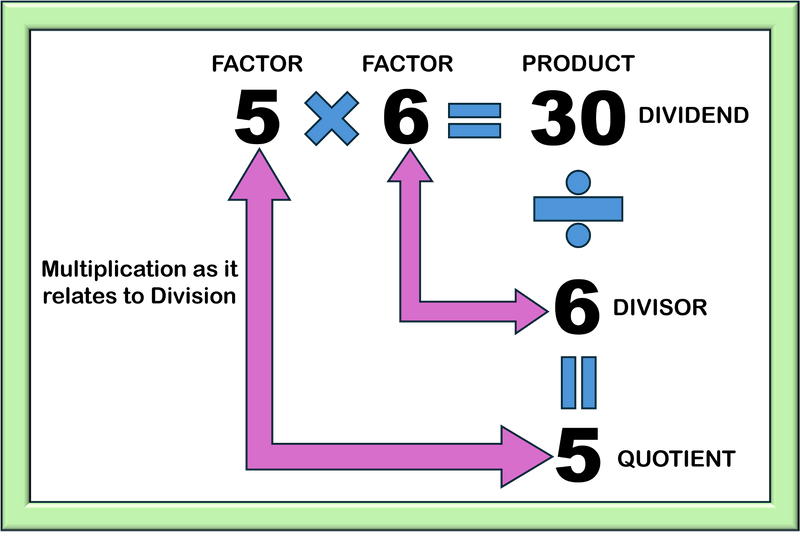Image created by Wendy F. McMillian

Explain how the factors 5 and 6 become the divisor and the quotient, and 30 becomes the dividend within the division problem.

Try this example with students:

You have 36 donuts that you want to divide between your 6 friends. How many donuts would each friend get?

• Help students think about the factors of 36: 1 x 36, 2 x 18, 3 x 12, 4 x 9, 6 x 6.

• Then ask: Which of these factors will work to divide the donuts evenly?

Answer: If you have 6 friends, and 6 x 6 is 36, each friend would get 6 donuts. So, 36 divided by 6 = 6.

AI-generated image created by Wendy F. McMillian

Show students how arrays relate to division and multiplication. Arrays are typically used for multiplication, but as you just learned, multiplication and division are opposites, so it makes sense that you can use an array to divide.

Use an example like the picture of eggs shown above. There are seven eggs in each row and six in each column. Multiplying these together gives us 42 (7 x 6 = 42).

Then have students think backward! For example: You have 42 eggs and want to make seven columns. How many rows would you need?

Think of the factors (the numbers that multiply together) that would give you 42: 42 x 1, 22 x 2, 14 x 3, 6 x 7.

Answer: There will be 6 rows. 7 and 6 are both factors of 42, so laying out the eggs in 6 rows of 7 will make 42 eggs.

Get students to solve a problem:

1. Give students 20 disks.

2. Ask them to divide the disks so that there are three rows with an equal number of disks in each row.

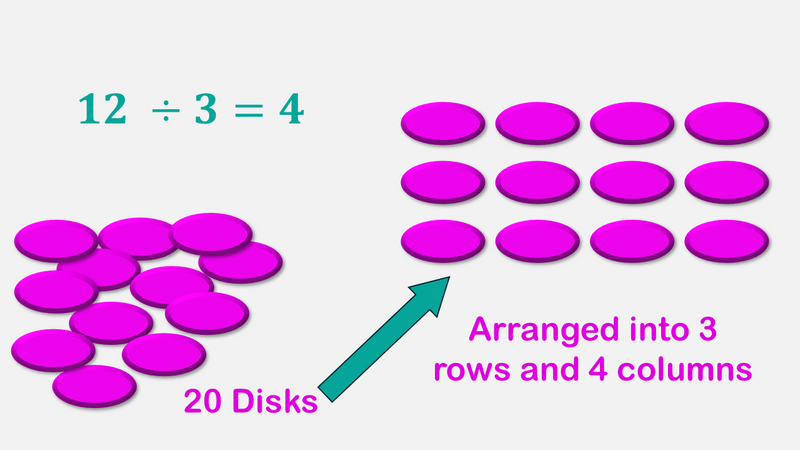Image created by Wendy F. McMillian

Students should conclude there will be four disks in each of the three rows of disks — 4 x 3 = 12, and 12 divided by 3 equals 4.

Clipart created by Wendy F. McMillian

After students learn that multiplication and division are opposites, they should be encouraged to know the multiplication tables since factors can easily be found that will multiply to get the number you're dividing.

Using the donut example, knowing the factors of 36 (1 x 36, 4 x 9, 6 x 6, 12 x 3, etc.) will help students divide 36 by one of its factors!

Teach students to use a multiplication table to find the factors of 36 easily.

Find 36 on the chart and follow the columns and rows until you find the factors of 36. You can divide 36 by any of these factors.

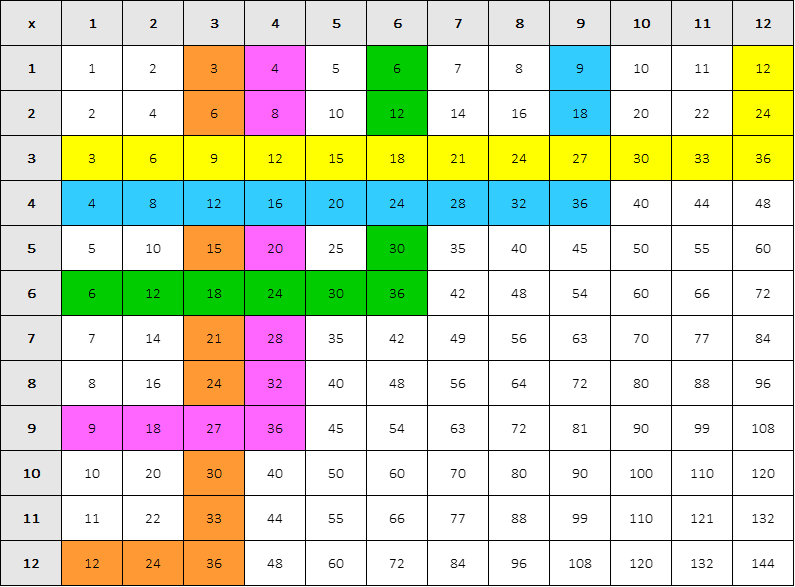Image created by Wendy F. McMillian

Teach students division rules:

First, they should know that dividing by powers of 10 is as simple as moving the decimal!

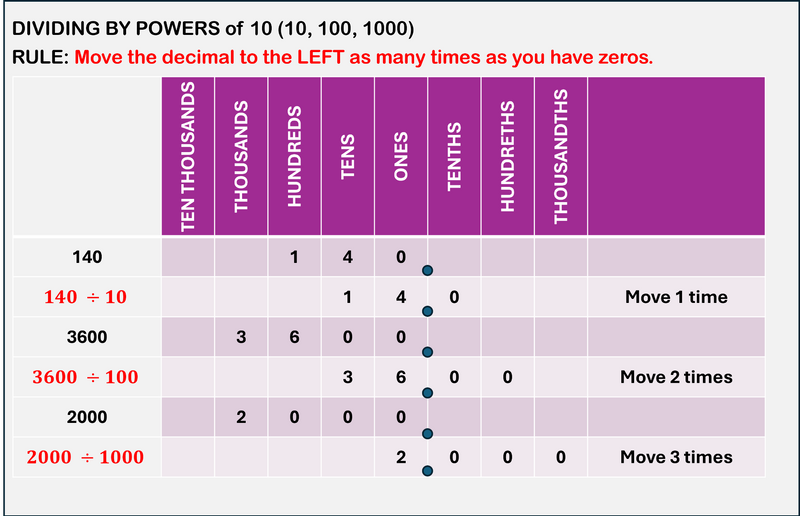Image created by Wendy F. McMillian

Secondly, students should know that each number follows its own divisibility rule!

Image created by Wendy F. McMillian

Post charts like these ones in your classroom for student reference.

Image created by Wendy F. McMillian

Now get out there and divide and conquer!