What's the difference between union and Intersection in math?

Your birthday is coming up, and you're making a guest list.

You want to invite friends from your soccer class and friends from your art class — and some are in both classes. Your mom asks how many guests are coming, so you add the total number from both classes. But wait...is that number really right?

Knowing the difference between union and intersection can help you in situations like this and many more!

In math, a set is a group or collection of things.

These things can be anything — like numbers, colors, people, objects, and so on.

We usually write sets within curly brackets { } separated by commas, and we don't repeat the same item more than once.

Examples:

• A set of numbers: {1, 2, 7, 10}

• A set of days: {Monday, Wednesday, Thursday}

• A set of students: {Sarah, Oscar, Andy, Thomas}

When we have two or more sets, the terms "union" and "intersection" help us see how they relate to each other.

Quick Check: Is It a Set?

A. {pizza, sandwich, cake}

B. {1, 4, 5, 5, 8, 10}

C. music and games

D. {March, May, June, October, December}

When we have two or more sets, a union is a combination of all the items, without repeating anything.

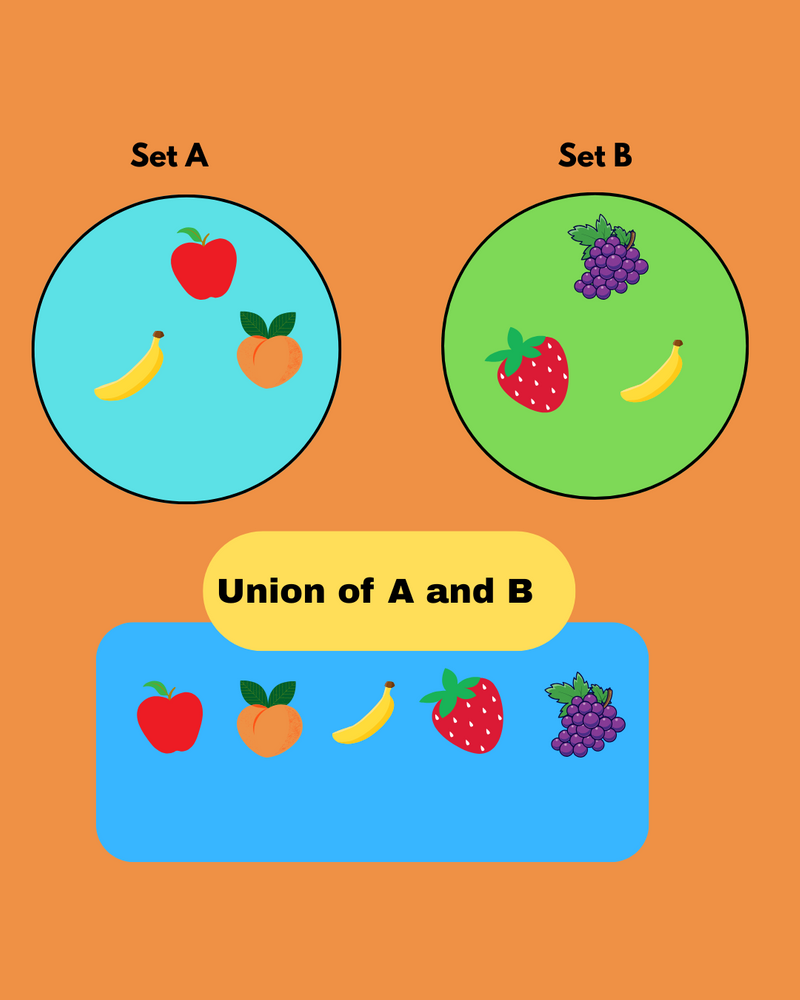Image created by the author via Canva

You can think of union as "OR" — as we include anything that is in one set or the other (or both).

But unlike just combining or adding the sets together, the union only includes each unique element once, even if it appears in both sets.

Here's an example:

Set A = {1, 3, 4}

Set B = {2, 4, 5, 6}

The union of Set A and Set B, written as A ∪ B, is {1, 2, 3, 4, 5, 6}.

Even though 4 appears in both sets, it appears only once in the union.📌

When we have two or more sets, an intersection means the items that are common to all the sets.

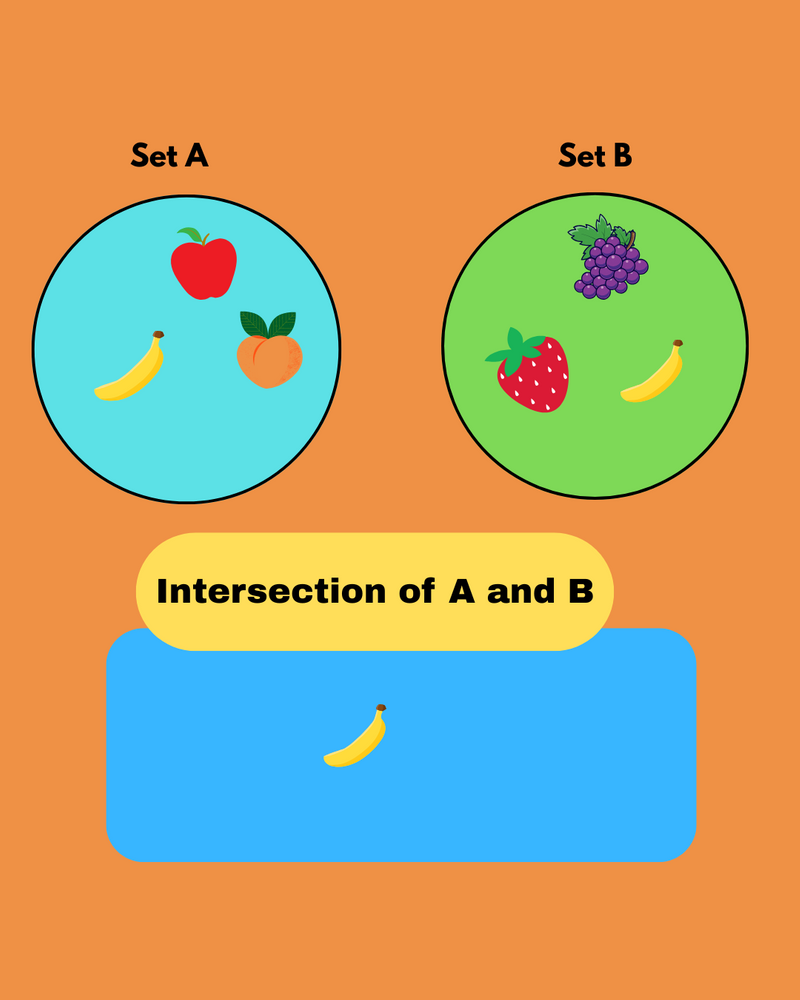Image created by the author via Canva

You can think of intersection as "AND" — as we only include the items that are in one set and the other.

Another example:

Set A = {1, 3, 4}

Set B = {1, 4, 5, 6}

The intersection of set A and set B, written as A ∩ B = {1, 4}.📌

Now that you know the difference between union and intersection, you decide to get creative about how to spend your birthday. Let's start planning!

You have two groups of friends:

• Soccer class friends: {Liam, Zoe, Victoria, Ryan}

• Art class friends: {Victoria, Ryan, Noah, Mark}

You want to organize two parties:

• Party 1: for all friends from both groups

• Party 2: for friends who are common across both groups

Which of the following are true?

A. Party 1 will have the union of the two groups, which is {Liam, Zoe, Victoria, Ryan, Noah, Mark}.

B. Party 2 will have only friends from art class, which is {Victoria, Ryan, Noah, Mark}.

C. Parties 1 and 2 will have an equal number of guests.

D. Party 2 will have the intersection of the two groups, which is {Liam, Zoe, Noah, Mark}.

A Venn diagram is a commonly used way to show how different sets are related, usually by drawing circles that may or may not overlap.

Let's represent the birthday party example using a Venn diagram:

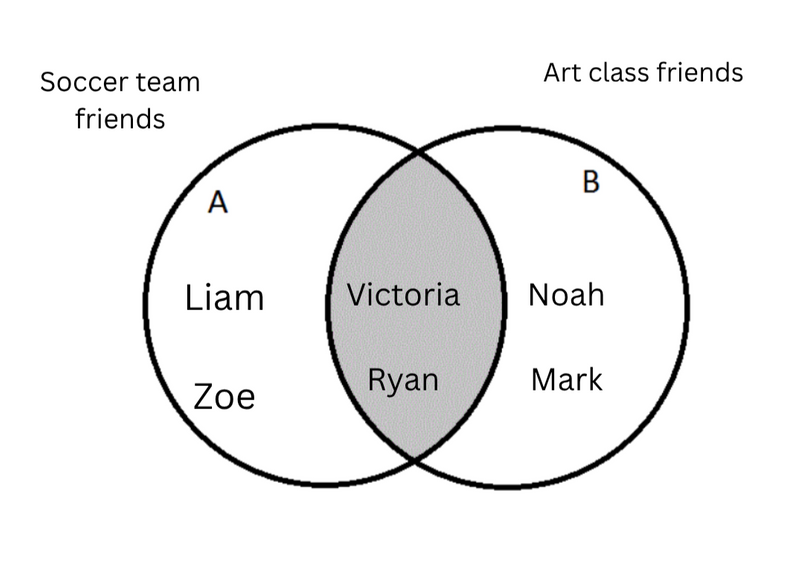Image created by the author via Canva

In the diagram...

• Each circle represents a set — one for soccer team friends, and another for art class friends.

• The union includes all names in either circle.

• The intersection is the overlapping part.

Here's another example:

If Set A= {5, 10, 15, 20, 25} and Set B= {10, 20, 30}. Here is a Venn diagram that shows the relation between Set A and Set B.

Union (A ∪ B): The shaded area shows all the elements that are either in A or B.

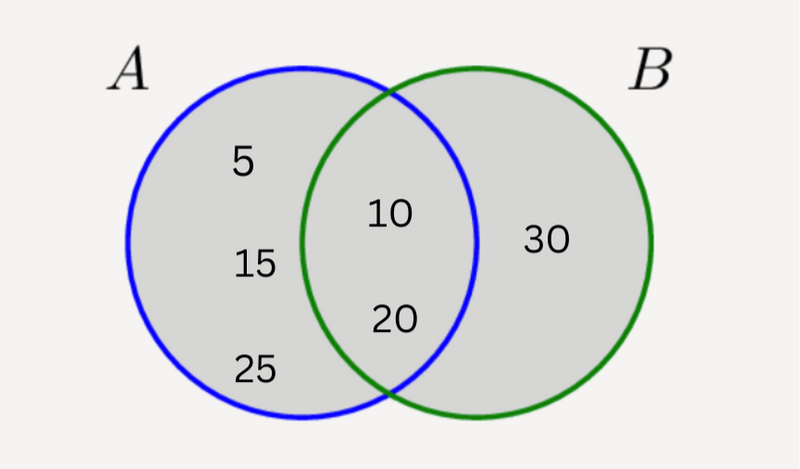A ∪ B = {5, 10, 15, 20, 25, 30}

Intersection (A ∩ B): The shaded area shows the elements in both A and B.

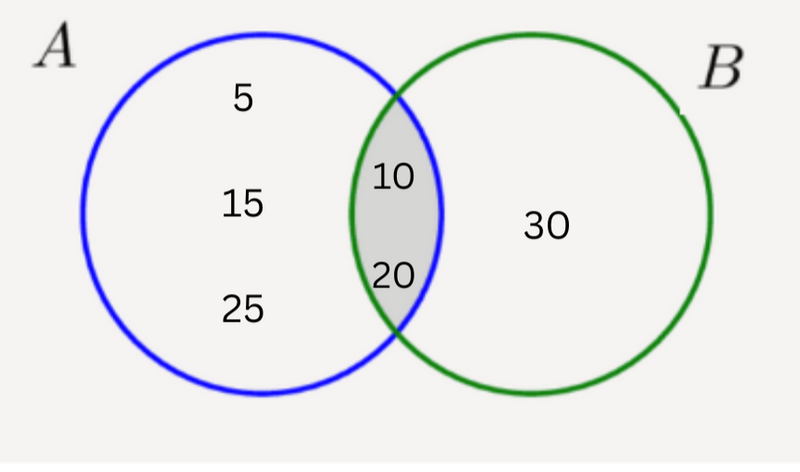A ∩ B = {10, 20}

Now that you understand the difference between union and intersection, take your learning a step further with these resources.